Пусть

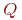1	0

Проверьте, истинно ли утверждение:

вопрос

Правильный ответ:

Оставить комментарий

Отправить

• # Пусть латинские буквы обозначают высказывания: A - общеутвердительное; E - общеотрицательное; O - частноотрицательное; I - частноутвердительное. Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X. Большая посылкаМалая посылкаФигура силлогизмаAA2
• # Пусть латинские буквы обозначают высказывания: A - общеутвердительное; E - общеотрицательное; O - частноотрицательное; I - частноутвердительное. Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X. Большая посылкаМалая посылкаФигура силлогизмаAE2
• # Как выглядит на языке кванторов утверждение: ""
• # Пусть 11 Проверьте, истинно ли утверждение:
• # Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме: \neg X_1 \wedge X_2 \wedge (X_2 \to X_3)= \vee_{\alpha_1, \alpha_2, \alpha_3}(A_{\alpha_1, \alpha_2, \alpha_3}X_1^{\alpha_1} \wedge X_2^{\alpha_2} \wedge X_3^{\alpha_3})\\ \mbox{где}\; X^{\alpha}=\begin{cases} X, & \mbox{если}\; \alpha =1,\\ \neg X, & \mbox{если}\; \alpha =0 \end{cases} может принимать значения 0 или 1. В ответе приведите значение для 101