Главная /
Введение в математические модели механики сплошных сред
Введение в математические модели механики сплошных сред - ответы на тесты Интуит
В курсе дается введение в основные математические понятия, используемые при построении моделей механики сплошных сред.
Список вопросов:
- # Перемещение - это ...
- # Скорость - это ...
- # Ускорение - это ...
- # Компоненты тензора деформаций с одинаковыми индексами для случая малых деформаций совпадают с:
- # Компоненты тензора деформаций с различными индексами для случая малых деформаций совпадают с:
- # Тензор деформации является:
- # Тензор деформации характеризует:
- # Тензор скоростей деформации характеризует:
- # Тензор деформации является:
- # Какие оси деформации называются главными?
- # Укажите верное определение для поверхности деформации Коши:
- # Тензор скоростей деформаций является:
- # Сдвиги в тензоре деформации по главным осях деформации:
- # Как называются деформации на главных осях деформации?
- # Какую часть полных деформаций характеризует шаровый тензор деформаций?
- # Какая величина является обобщенной интегральной характеристикой сдвиговых деформаций в окрестности индивидуальной точки?
- # Какие величины характеризуют изменение объема индивидуальных частиц материального континуума?
- # Какую часть полных деформаций характеризует девиатор тензора деформаций?
-
#
Вычислить компоненту
![math]() тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат ![math]() для течений среды с полями скорости, имеющими в этих координатах компоненты:
для течений среды с полями скорости, имеющими в этих координатах компоненты: ![math]() ,
,![math]() ,
,![math]() , где
, где ![math]()
-
#
Вычислить компоненту
![math]() тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат ![math]() для течений среды с полями скорости, имеющими в этих координатах компоненты:
для течений среды с полями скорости, имеющими в этих координатах компоненты: ![math]() ,
,![math]() ,
,![math]() , где
, где ![math]()
-
#
Вычислить компоненту
![math]() девиатора тензора скоростей деформаций
девиатора тензора скоростей деформаций ![math]() в пространственной декартовой системе координат
в пространственной декартовой системе координат ![math]() для течений среды с полями скорости, имеющими в этих координатах компоненты:
для течений среды с полями скорости, имеющими в этих координатах компоненты: ![math]() ,
,![math]() ,
,![math]() , где
, где ![math]()
- # В некоторой точке среды, в которой произошла малая деформация, тензор малых деформаций в декартовой системе координат имеет следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} {0,01} & {0,03} & 0 \\ {0,03} & {0,01} & 0 \\ 0 & 0 & {0,01} \\ \end{array}} \right) Найти наибольшее относительчое удлинение материальных элементов в этой точке
- # В некоторой точке среды, в которой произошла малая деформация, тензор малых деформаций в декартовой системе координат имеет следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} {0,01} & {0,03} & 0 \\ {0,03} & {0,01} & 0 \\ 0 & 0 & {0,01} \\ \end{array}} \right) Найти наименьшее относительчое удлинение материальных элементов в этой точке
- # В некоторой точке среды, в которой произошла малая деформация, тензор малых деформаций в декартовой системе координат имеет следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} {0,01} & {0,03} & 0 \\ {0,03} & {0,01} & 0 \\ 0 & 0 & {0,01} \\ \end{array}} \right) Найти направление материальных элементов, которые испытали наибольшее относительное удлинение
-
#
Вычислить компоненту
![math]() девиатора тензора скоростей деформаций
девиатора тензора скоростей деформаций ![math]() в пространственной декартовой системе координат
в пространственной декартовой системе координат ![math]() для течений среды с полями скорости, имеющими в этих координатах компоненты:
для течений среды с полями скорости, имеющими в этих координатах компоненты: ![math]() ,
,![math]() ,
,![math]() , где
, где ![math]()
-
#
Вычислить компоненту
![math]() девиатора тензора скоростей деформаций
девиатора тензора скоростей деформаций ![math]() в пространственной декартовой системе координат
в пространственной декартовой системе координат ![math]() для течений среды с полями скорости, имеющими в этих координатах компоненты:
для течений среды с полями скорости, имеющими в этих координатах компоненты: ![math]() ,
,![math]() ,
,![math]() , где
, где ![math]()
-
#
Вычислить компоненту
![math]() тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат ![math]() для течений среды с полями скорости, имеющими в этих координатах компоненты:
для течений среды с полями скорости, имеющими в этих координатах компоненты: ![math]() ,
,![math]() , где
, где ![math]()
- # В некоторой точке среды, в которой произошла малая деформация, тензор малых деформаций в декартовой системе координат имеет следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} {0,01} & {0,03} & 0 \\ {0,03} & {0,01} & 0 \\ 0 & 0 & {0,01} \\ \end{array}} \right) Найти направление материальных элементов, которые испытали наименьшее относительное удлинение
- # В некоторой точке среды, в которой произошла малая деформация, тензор малых деформаций в декартовой системе координат имеет следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} {0,01} & {0,03} & 0 \\ {0,03} & {0,01} & 0 \\ 0 & 0 & {0,01} \\ \end{array}} \right) Вычислить относительное изменение объема в этой точке
-
#
Вычислить компоненту
![math]() тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат ![math]() для течения среды с полем скорости, имеющим в этой системе координат компоненты:
для течения среды с полем скорости, имеющим в этой системе координат компоненты: ![math]() ,
,![math]() ,
,![math]()
-
#
Вычислить компоненту
![math]() девиатора тензора скоростей деформаций
девиатора тензора скоростей деформаций ![math]() в пространственной декартовой системе координат
в пространственной декартовой системе координат ![math]() для течений среды с полями скорости, имеющими в этих координатах компоненты:
для течений среды с полями скорости, имеющими в этих координатах компоненты: ![math]() ,
,![math]() , где
, где ![math]()
-
#
Вычислить компоненту
![math]() девиатора тензора скоростей деформаций
девиатора тензора скоростей деформаций ![math]() в пространственной декартовой системе координат
в пространственной декартовой системе координат ![math]() для течений среды с полями скорости, имеющими в этих координатах компоненты:
для течений среды с полями скорости, имеющими в этих координатах компоненты: ![math]() ,
,![math]() , где
, где ![math]()
-
#
Вычислить компоненту
![math]() девиатора тензора скоростей деформаций
девиатора тензора скоростей деформаций ![math]() в пространственной декартовой системе координат
в пространственной декартовой системе координат ![math]() для течений среды с полями скорости, имеющими в этих координатах компоненты:
для течений среды с полями скорости, имеющими в этих координатах компоненты: ![math]() ,
,![math]() , где
, где ![math]()
-
#
Вычислить компоненту
![math]() тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат ![math]() для течения среды с полем скорости, имеющим в этой системе координат компоненты:
для течения среды с полем скорости, имеющим в этой системе координат компоненты: ![math]() ,
,![math]() ,
,![math]()
-
#
Вычислить компоненту
![math]() тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат ![math]() для течения среды с полем скорости, имеющим в этой системе координат компоненты:
для течения среды с полем скорости, имеющим в этой системе координат компоненты: ![math]() ,
,![math]() ,
,![math]()
-
#
Вычислить компоненту
![math]() тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат ![math]() для течений среды с полями скорости, имеющими в этих координатах компоненты:
для течений среды с полями скорости, имеющими в этих координатах компоненты: ![math]() ,
,![math]() , где
, где ![math]()
- # Укажите закон сохранения масс:
- # Укажите закон сохранения импульса:
- # Укажите закон изменения момента количества движения:
- # Сплошная среда является несжимаемой, если:
- # Сплошная среда является однородной в том случае, если:
- # На какие составляющие может быть разложена субстациональная производная по времени?
- # Поверхностные силы - это ...
- # Массовые силы - это
- # Локальная производная определяется:
- # Сила трения является:
- # Сила давления является:
- # Сила тяжести является:
- # Тензор напряжений является:
- # Тензор напряжений является:
- # Какую часть полных напряжений характеризует шаровый тензор напряжений?
- # Площадки, на которых отсутствуют касательные напряжения, называются:
- # Какие скалярные величины определяют вектор полного напряжения в точке:
- # Какую часть полных напряжений характеризует девиатор тензора напряжений?
-
#
В некоторой точке тела в декартовой ортогональной системе координат тензор напряжений задан своими компонентами (в Паскалях): ({p^{ij}}) = \left( {\begin{array}{*{20}{c}}
{100} & {100} & {160} \\
{100} & 0 & { - 150} \\
{160} & { - 150} & { - 60} \\
\end{array}} \right) Для площадки с нормалью
![math]() ,
,![math]() ,
,![math]() , найти компоненту
, найти компоненту ![math]() вектора
вектора ![math]()
-
#
В некоторой точке тела в декартовой ортогональной системе координат тензор напряжений задан своими компонентами (в Паскалях): ({p^{ij}}) = \left( {\begin{array}{*{20}{c}}
{100} & {100} & {160} \\
{100} & 0 & { - 150} \\
{160} & { - 150} & { - 60} \\
\end{array}} \right) Для площадки с нормалью
![math]() ,
,![math]() ,
,![math]() , найти компоненту
, найти компоненту ![math]() вектора
вектора ![math]()
-
#
В некоторой точке тела в декартовой ортогональной системе координат тензор напряжений задан своими компонентами (в Паскалях): ({p^{ij}}) = \left( {\begin{array}{*{20}{c}}
{100} & {100} & {160} \\
{100} & 0 & { - 150} \\
{160} & { - 150} & { - 60} \\
\end{array}} \right) Для площадки с нормалью
![math]() ,
,![math]() ,
,![math]() , найти компоненту
, найти компоненту ![math]() вектора
вектора ![math]()
-
#
В декартовой системе координат компоненты тензора напряжений в точке М таковы:
![math]() ,
,![math]() ,
,![math]() ,
,![math]() Определить главный компонент
Определить главный компонент ![math]() тензора напряжений
тензора напряжений
-
#
В декартовой системе координат компоненты тензора напряжений в точке М таковы:
![math]() ,
,![math]() ,
,![math]() ,
,![math]() Определить главный компонент
Определить главный компонент ![math]() тензора напряжений
тензора напряжений
-
#
В декартовой системе координат компоненты тензора напряжений в точке М таковы:
![math]() ,
,![math]() ,
,![math]() ,
,![math]() Определить главный компонент
Определить главный компонент ![math]() тензора напряжений
тензора напряжений
-
#
В некоторой точке тела в декартовой ортогональной системе координат тензор напряжений задан своими компонентами (в Паскалях): ({p^{ij}}) = \left( {\begin{array}{*{20}{c}}
{100} & {100} & {160} \\
{100} & 0 & { - 150} \\
{160} & { - 150} & { - 60} \\
\end{array}} \right) Для площадки с нормалью
![math]() ,
,![math]() ,
,![math]() , найти величину касательного напряжения
, найти величину касательного напряжения ![math]()
-
#
В некоторой точке тела в декартовой ортогональной системе координат тензор напряжений задан своими компонентами (в Паскалях): ({p^{ij}}) = \left( {\begin{array}{*{20}{c}}
{100} & {100} & {160} \\
{100} & 0 & { - 150} \\
{160} & { - 150} & { - 60} \\
\end{array}} \right) Для площадки с нормалью
![math]() ,
,![math]() ,
,![math]() , найти величину нормального напряжения
, найти величину нормального напряжения ![math]()
-
#
В некоторой точке тела в декартовой ортогональной системе координат тензор напряжений задан своими компонентами (в Паскалях): ({p^{ij}}) = \left( {\begin{array}{*{20}{c}}
{100} & {100} & {160} \\
{100} & 0 & { - 150} \\
{160} & { - 150} & { - 60} \\
\end{array}} \right) Для площадки с нормалью
![math]() ,
,![math]() ,
,![math]() , найти величину
, найти величину ![math]()
-
#
В декартовой системе координат компоненты тензора напряжений в точке М таковы:
![math]() ,
,![math]() ,
,![math]() ,
,![math]() Определить, какой из перечисленных ниже направляющих косинусов, соответствует главной оси тензора напряжений
Определить, какой из перечисленных ниже направляющих косинусов, соответствует главной оси тензора напряжений
-
#
В декартовой системе координат компоненты тензора напряжений в точке М таковы:
![math]() ,
,![math]() ,
,![math]() ,
,![math]() Определить, какой из перечисленных ниже направляющих косинусов, соответствует главной оси тензора напряжений
Определить, какой из перечисленных ниже направляющих косинусов, соответствует главной оси тензора напряжений
-
#
В декартовой системе координат компоненты тензора напряжений в точке М таковы:
![math]() ,
,![math]() ,
,![math]() ,
,![math]() Определить, какой из перечисленных ниже направляющих косинусов, соответствует главной оси тензора напряжений
Определить, какой из перечисленных ниже направляющих косинусов, соответствует главной оси тензора напряжений
-
#
В некоторой точке тела в декартовой ортогональной системе координат тензор напряжений задан своими компонентами (в Паскалях): ({p^{ij}}) = \left( {\begin{array}{*{20}{c}}
{100} & {100} & {160} \\
{100} & 0 & { - 150} \\
{160} & { - 150} & { - 60} \\
\end{array}} \right) Для площадки с нормалью
![math]() ,
,![math]() ,
,![math]() , найти угол
, найти угол ![math]() между
между ![math]() и
и ![math]()
-
#
В некоторой точке тела в декартовой ортогональной системе координат тензор напряжений задан своими компонентами (в Паскалях): ({p^{ij}}) = \left( {\begin{array}{*{20}{c}}
{100} & {100} & {160} \\
{100} & 0 & { - 150} \\
{160} & { - 150} & { - 60} \\
\end{array}} \right) Для площадки с нормалью
![math]() ,
,![math]() ,
,![math]() , найти косинус угла
, найти косинус угла ![math]() между
между ![math]() и
и ![math]()
-
#
В точке М в декартовой системе координат компоненты тензора напряжений заданы матрицей: ({p^{ij}}) = \left( {\begin{array}{*{20}{c}}
8 & 0 & { - 4} \\
0 & 5 & 0 \\
{ - 4} & 0 & 4 \\
\end{array}} \right) Определить вектор напряжений
![math]() на площадке с нормалью
на площадке с нормалью ![math]()
-
#
Симметричный тензор напряжений в некоторой точке в декартовой ортогональной системе координат имеет компоненты:
![math]() ,
,![math]() . Здесь значения
. Здесь значения ![math]() отнесены к некоторому характерному значению напряжения
отнесены к некоторому характерному значению напряжения ![math]() и приведены в безразмерном виде. Определить главный компонент
и приведены в безразмерном виде. Определить главный компонент ![math]() тензора напряжений
тензора напряжений
-
#
Симметричный тензор напряжений в некоторой точке в декартовой ортогональной системе координат имеет компоненты:
![math]() ,
,![math]() . Здесь значения
. Здесь значения ![math]() отнесены к некоторому характерному значению напряжения
отнесены к некоторому характерному значению напряжения ![math]() и приведены в безразмерном виде. Определить главный компонент
и приведены в безразмерном виде. Определить главный компонент ![math]() тензора напряжений
тензора напряжений
-
#
Симметричный тензор напряжений в некоторой точке в декартовой ортогональной системе координат имеет компоненты:
![math]() ,
,![math]() . Здесь значения
. Здесь значения ![math]() отнесены к некоторому характерному значению напряжения
отнесены к некоторому характерному значению напряжения ![math]() и приведены в безразмерном виде. Определить главный компонент
и приведены в безразмерном виде. Определить главный компонент ![math]() тензора напряжений
тензора напряжений
- # Укажите первый закон термодинамики:
- # Укажите второй закон термодинамики:
- # Вектор теплового потока характеризует:
- # Дифференциальное уравнение энергии устанавливает, что:
- # Укажите теорему "живых сил"
- # Укажите закон сохранения энергии при отсутствии тепловых явлений:
- # При наличии тепловых явлений внутренняя энергия тела в целом представляет собой:
- # Вектор теплового потока по модулю равен:
- # Укажите закон теплопроводности Фурье:
- # Энтропия характеризует:
- # Необратимые процессы — это ...
- # Обратимые процессы — это ...
- # В изолированной системе реальные процессы могут протекать в сторону перехода:
- # В изолированной системе реальные процессы могут протекать сопровождаясь:
- # В изолированной системе реальные процессы могут протекать при:
- # Адиабатические процессы - это ...
- # Формальным выражением условия адиабатичности процесса является:
- # При адиабатическом деформировании сплошной среды, энтропия частиц среды может:
- # Процессы, происходящие в отсутствие теплообмена как между различными частицами сплошной среды, так и с окружающей данное тело средой, называются:
- # Формальным выражением условия какого процесса является равенство нулю дивергенции вектора теплового потока?
- # Какая величина характеризует направление наиболее интенсивной передачи тепловой энергии в окрестности точки сплошной среды?
- # Укажите формулу закона теплопроводности Фурье:
- # Какой из видов теплообмена реализуется в любых сплошных средах независимо от их агрегатного состояния и физико-механических свойств?
- # Укажите формулу энтропии:
- # Камень массой 5 кг, имеющий температуру 473 K, опускают в сосуд, содержащий 9 кг воды при 5°С. Удельная теплоемкость камня 0,2 кал/(г*град). Найти конечную температуру, не учитывая потери тепла через стенки сосуда
- # Сколько килограммов воздуха содержится в комнате размером 20 x 20 x 3 м при нормальных условиях: температура 20°С, давление 1 атм? Воздух считать совершенным газом, для воздуха R = 287,042 м2/(с2*град)
- # Пар впускается в цилиндр машины при постоянном давлении 20 атм. Ход поршня 60 см, его диаметр 20 см. Какую работу (в джоулях) совершает пар за один полный ход поршня?
-
#
Для увеличения площади поверхности жидкости на величину
![math]() необходимо из-за наличия поверхностного натяжения совершить работу
необходимо из-за наличия поверхностного натяжения совершить работу ![math]() , где
, где ![math]() — коэффициент поверхностного натяжения. Какую работу необходимо затратить, чтобы разделить 1 л воды на капли диаметром 0,01 мм? Принять, что
— коэффициент поверхностного натяжения. Какую работу необходимо затратить, чтобы разделить 1 л воды на капли диаметром 0,01 мм? Принять, что ![math]()
-
#
Для увеличения площади поверхности жидкости на величину
![math]() необходимо из-за наличия поверхностного натяжения совершить работу
необходимо из-за наличия поверхностного натяжения совершить работу ![math]() , где
, где ![math]() — коэффициент поверхностного натяжения. На сколько градусов можно поднять температуру 1 л воды перемешиванием за счет количества работы, которого необходимо затратить, чтобы разделить 1 л воды на капли диаметром 0,01 мм? Принять, что
— коэффициент поверхностного натяжения. На сколько градусов можно поднять температуру 1 л воды перемешиванием за счет количества работы, которого необходимо затратить, чтобы разделить 1 л воды на капли диаметром 0,01 мм? Принять, что ![math]() , потери тепла во внешнюю среду не учитывать
, потери тепла во внешнюю среду не учитывать
-
#
Для увеличения площади поверхности жидкости на величину
![math]() необходимо из-за наличия поверхностного натяжения совершить работу
необходимо из-за наличия поверхностного натяжения совершить работу ![math]() , где
, где ![math]() — коэффициент поверхностного натяжения. На какую высоту можно поднять 1 л воды с помощью количества работы, которого необходимо затратить, чтобы разделить 1 л воды на капли диаметром 0,01 мм? Принять, что
— коэффициент поверхностного натяжения. На какую высоту можно поднять 1 л воды с помощью количества работы, которого необходимо затратить, чтобы разделить 1 л воды на капли диаметром 0,01 мм? Принять, что ![math]()
- # Найти стационарное распределение температуры в однородном покоящемся слое сплошной среды с постоянной теплопроводностью, расположенной между двумя бесконечными параллельными пластинами с постоянными температурами Т1 и Т2 соответственно. Толщина слоя равна h
- # Термос заполнен смесью льда и воды. Поскольку изоляция термоса неидеальна, лед постепенно тает. Однако таяние происходит медленно, температура в термосе остается практически неизменной и равной 0°С. Вычислить изменение энтропии, соответствующее таянию 500 г льда. Теплота плавления льда равна 79,67 кал/г
- # Термос заполнен смесью льда и воды. Поскольку изоляция термоса неидеальна, лед постепенно тает. Однако таяние происходит медленно, температура в термосе остается практически неизменной и равной 0°С. Теплота плавления льда равна 79,67 кал/г. Как изменится энтропия 500 г воды при превращении ее в лед при температуре 0°С?
- # Вычислить изменение энтропии 500 г воды при ее испарении при 100°С (при кипении). Теплота испарения при такой температуре равна 539 кал/г
-
#
Чему равно изменение энтропии упругого стального стержня, длина которого 1 м, площадь поперечного сечения 1 см2, при его изотермическом растяжении до 1,001 м при температуре 15°С. Считать, что для стали модуль Юнга
![math]() , коэффициент Пуассона
, коэффициент Пуассона ![math]() , удельная теплоемкость при постоянных деформациях
, удельная теплоемкость при постоянных деформациях ![math]() , коэффициент линейного теплового расширения
, коэффициент линейного теплового расширения ![math]() . Модуль Юнга и коэффициент Пуассона выражаются через коэффициенты Ламе по формулам:
. Модуль Юнга и коэффициент Пуассона выражаются через коэффициенты Ламе по формулам: ![math]() ,
,![math]()
-
#
Чему равна величина растягивающей силы упругого стального стержня, длина которого 1 м, площадь поперечного сечения 1 см2, при его изотермическом растяжении до 1,001 м при температуре 15°С. Считать, что для стали модуль Юнга
![math]() , коэффициент Пуассона
, коэффициент Пуассона ![math]() , удельная теплоемкость при постоянных деформациях
, удельная теплоемкость при постоянных деформациях ![math]() , коэффициент линейного теплового расширения
, коэффициент линейного теплового расширения ![math]() . Модуль Юнга и коэффициент Пуассона выражаются через коэффициенты Ламе по формулам:
. Модуль Юнга и коэффициент Пуассона выражаются через коэффициенты Ламе по формулам: ![math]() ,
,![math]()
- # Идеальная среда — это ...
- # В идеальной среде:
- # Идеальная среда ...
- # Каким оказывается тензор напряжений в любой индивидуальной частице идеального газа?
- # Идеальный газ ...
- # Как называется среда, не способная оказывать сопротивление изменению формы своих частиц?
- # Идеальная баротпропная среда - это ...
- # Давление в идеальной баротпропной среде не зависит от:
- # Как называется среда, давление в которой зависит лишь от плотности, не принимая во внимание зависимость давления от температуры?
- # Уравнения Эйлера для идеальной среды представляют собой частный случай:
- # Деформирование идеальной среды в адиабатических условиях происходит:
- # Какие уравнения выражают собой частный случай закона сохранения импульса для деформируемой идеальной среды?
-
#
Укажите условие, которое должно быть выполнено для потенциального движения сплошной среды(
![math]() -вектор скорости,
-вектор скорости, ![math]() -потенциал скорости):
-потенциал скорости):
-
#
Для потенциального движения сплошной среды выполнено(
![math]() -вектор скорости,
-вектор скорости, ![math]() -потенциал скорости):
-потенциал скорости):
-
#
Какие условия должны выполняться для потенциального движения сплошной среды?(
![math]() -вектор скорости,
-вектор скорости, ![math]() -потенциал скорости)
-потенциал скорости)
-
#
Укажите условие, которое должно быть выполнено для вихревого движения сплошной среды(
![math]() -вектор скорости,
-вектор скорости, ![math]() -потенциал скорости):
-потенциал скорости):
- # Потенциальное движение среды называется осесимметричным, если:
- # Движение среды называется плоским, если
-
#
Выразить через функцию тока
![math]() расход жидкости
расход жидкости ![math]() через криволинейную дугу, соединяющую точки с координатами
через криволинейную дугу, соединяющую точки с координатами ![math]() и
и ![math]()
-
#
Найти потенциал скорости для течения, задаваемого комплексным потенциалом:
![math]()
-
#
Найти функцию тока для течения, задаваемого комплексным потенциалом:
![math]()
-
#
Через функцию тока
![math]() выразить физическую компоненту скорости
выразить физическую компоненту скорости ![math]() в правой ортогональной криволинейной системе координат
в правой ортогональной криволинейной системе координат ![math]() , где
, где ![math]() — координаты в плоскости меридиана,
— координаты в плоскости меридиана, ![math]() — угол, определяющий положение плоскости меридиана.
— угол, определяющий положение плоскости меридиана. ![math]() - параметры Ламе
- параметры Ламе
-
#
Через функцию тока
![math]() выразить физическую компоненту скорости
выразить физическую компоненту скорости ![math]() в правой ортогональной криволинейной системе координат
в правой ортогональной криволинейной системе координат ![math]() , где
, где ![math]() — координаты в плоскости меридиана,
— координаты в плоскости меридиана, ![math]() — угол, определяющий положение плоскости меридиана.
— угол, определяющий положение плоскости меридиана. ![math]() - параметры Ламе
- параметры Ламе
-
#
Через функцию тока
![math]() выразить физические компоненты вихря скорости в правой ортогональной криволинейной системе координат
выразить физические компоненты вихря скорости в правой ортогональной криволинейной системе координат ![math]() , где
, где ![math]() — координаты в плоскости меридиана,
— координаты в плоскости меридиана, ![math]() — угол, определяющий положение плоскости меридиана.
— угол, определяющий положение плоскости меридиана. ![math]() - параметры Ламе
- параметры Ламе
-
#
Найти потенциал скорости для течения, задаваемого комплексным потенциалом:
![math]()
-
#
Найти функцию тока для течения, задаваемого комплексным потенциалом:
![math]()
-
#
Найти потенциал скорости для течения, задаваемого комплексным потенциалом:
![math]()
-
#
Через функцию тока
![math]() выразить физическую компоненту скорости
выразить физическую компоненту скорости ![math]() в цилиндрической системе координат
в цилиндрической системе координат ![math]()
-
#
Через функцию тока
![math]() выразить физическую компоненту скорости
выразить физическую компоненту скорости ![math]() в цилиндрической системе координат
в цилиндрической системе координат ![math]()
-
#
Через функцию тока
![math]() выразить физические компоненты вихря скорости в цилиндрической системе координат
выразить физические компоненты вихря скорости в цилиндрической системе координат ![math]()
-
#
Найти функцию тока для течения, задаваемого комплексным потенциалом:
![math]()
-
#
Найти потенциал скорости для течения, задаваемого комплексным потенциалом:
![math]()
-
#
Найти функцию тока для течения, задаваемого комплексным потенциалом:
![math]()
-
#
Через функцию тока
![math]() выразить физическую компоненту скорости
выразить физическую компоненту скорости ![math]() в сферической системе координат
в сферической системе координат ![math]()
-
#
Через функцию тока
![math]() выразить физическую компоненту скорости
выразить физическую компоненту скорости ![math]() в сферической системе координат
в сферической системе координат ![math]()
-
#
Через функцию тока
![math]() выразить физические компоненты вихря скорости в сферической системе координат
выразить физические компоненты вихря скорости в сферической системе координат ![math]()
- # Укажите количество угловых координат в декартовой прямоугольной системе координат:
- # Укажите количество угловых координат в цилиндрической системе координат:
- # Укажите количество угловых координат в сферической системе координат:
- # Координатная линия - это геометрическое место точек в пространстве, характеризуемое ...
- # Координатная поверхность - это геометрическое место точек в пространстве, характеризуемое ...
- # Укажите, какая из перечисленных ниже систем координат, является прямолинейной?
- # Скалярное произведение векторов основного и взаимного базиса с разными индексами равно:
- # Скалярное произведение векторов основного и взаимного базиса с одинаковыми индексами равно:
- # Укажите, какие из перечисленных ниже систем координат, являются криволинейными?
- # Какую особенность необходимо учитывать при дифференцировании тензоров прямоугольной системы координат?
- # Какую особенность необходимо учитывать при дифференцировании тензоров криволинейной системы координат?
- # Базисные векторы являются функциями:
- # Символы Кристоффеля второго рода - это ...
- # Символы Кристоффеля первого рода - это ...
- # Символы Кристоффеля ...
- # Укажите соотношение векторов основного и взаимного базиса системы координат при i=j:
- # Укажите соотношение векторов основного и взаимного базиса системы координат при i≠j:
- # Символы Кристоффеля первого и второго рода являются:
- # Выписать подробно выражение tii, используя числовые значения индексов, а не их буквенные обозначения:
- # Выписать подробно выражение Zii, используя числовые значения индексов, а не их буквенные обозначения:
- # Выписать подробно выражение Pii, используя числовые значения индексов, а не их буквенные обозначения:
- # Указать равные между собой выражения: 1) pijuj 2) ujpij 3) pijui 4) uipij
- # Указать равные между собой выражения: 1) qijaibj 2) qijbjai 3) bjqijai 4) aiqijbj
- # Указать равные между собой выражения: 1) aibjqij 2) bjaiqij 3) qijajbi
- # Вычислить сумму выражения δii
- # Вычислить сумму выражения δijδji
- # Вычислить сумму выражения δijδjkδki
- # Вычислить сумму выражения δii, если все индексы пробегают значения 1,2,...,n
- # Вычислить сумму выражения δijδji, если все индексы пробегают значения 1,2,...,n
- # Вычислить сумму выражения δijδjkδki, если все индексы пробегают значения 1,2,...,n
- # Вычислить сумму выражения pijuj при i=1
- # Вычислить сумму выражения pijuj при i=2
- # Вычислить сумму выражения pijuj при i=3
- # Вычислить сумму выражения pijui при j=1
- # Вычислить сумму выражения pij*ui при j=2
- # Вычислить сумму выражения pijui при j=3
- # Как называются величины, преобразующиеся при переходе от одной системы координат к другой, подобно компонентам вектора dr в разложении по векторам основного базиса?
- # Как называются величины, преобразующиеся при переходе от одной системы координат к другой, подобно векторам основного базиса?
- # У ковариантной величины индекс:
- # По какому закону проводится преобразование координат?
- # По какому закону проводится преобразование векторов основного базиса при переходе от одной системы координат к другой?
- # Ковариантный и контрвариантный законы преобразования являются:
- # У контрвариантной величины индекс:
- # Скалярным произведением тензоров первого ранга является:
- # При скалярном умножении тензоров, результирующий тензор имеет ранг, равный:
- # Скалярное произведение двух векторов определяется как ...
- # Векторное произведение двух векторов определяется как ...
- # Векторные величины ...
- # Дискриминантный тензор является тензором:
- # При векторном умножении тензоров, результирующий тензор имеет ранг, равный:
- # Результатом умножения тензора на скалярную величину будет тензор:
- # Сколько компонент имеет тензор нулевого ранга?
- # Сколько компонент имеет тензор первого ранга?
- # Сколько компонент имеет тензор второго ранга?
- # Равны ли свертки ijuiuj и tijuiuj, где ui - компоненты векторов
- # Равны ли свертки ijuivj и tijuivj, где ui,vj - компоненты векторов
- # Равны ли свертки ijuiuj и tijuivj, где ui,vj - компоненты векторов
-
#
Найти главный компонент тензора
![math]() , имеющего в некотором ортонормированном базисе еi следующую матрицу компонент:
\left( {\begin{array}{*{20}{c}}
1 & { - \sqrt 3 } & 0 \\
{ - \sqrt 3 } & { - 1} & 0 \\
0 & 0 & 3 \\
\end{array}} \right)
, имеющего в некотором ортонормированном базисе еi следующую матрицу компонент:
\left( {\begin{array}{*{20}{c}}
1 & { - \sqrt 3 } & 0 \\
{ - \sqrt 3 } & { - 1} & 0 \\
0 & 0 & 3 \\
\end{array}} \right)
- # Найти главный компонент тензора 2, имеющего в некотором ортонормированном базисе е1 следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} 1 & { - \sqrt 3 } & 0 \\ { - \sqrt 3 } & { - 1} & 0 \\ 0 & 0 & 3 \\ \end{array}} \right)
- # Найти главный компонент тензора 3, имеющего в некотором ортонормированном базисе е1 следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} 1 & { - \sqrt 3 } & 0 \\ { - \sqrt 3 } & { - 1} & 0 \\ 0 & 0 & 3 \\ \end{array}} \right)
- # Найти главный компонент тензора 1, имеющего в некотором ортонормированном базисе е1 следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} 1 & { - \sqrt 3 } & 0 \\ { - \sqrt 3 } & { - 1} & 0 \\ 0 & 0 & 2 \\ \end{array}} \right)
- # Найти главный компонент тензора 2, имеющего в некотором ортонормированном базисе е1 следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} 1 & { - \sqrt 3 } & 0 \\ { - \sqrt 3 } & { - 1} & 0 \\ 0 & 0 & 2 \\ \end{array}} \right)
- # Найти главный компонент тензора 3, имеющего в некотором ортонормированном базисе е1 следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} 1 & { - \sqrt 3 } & 0 \\ { - \sqrt 3 } & { - 1} & 0 \\ 0 & 0 & 2 \\ \end{array}} \right)
- # Указать вдоль какого из векторов направлена главная ось тензора, имеющего в некотором ортонормированном базисе е1 следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} 1 & { - \sqrt 3 } & 0 \\ { - \sqrt 3 } & { - 1} & 0 \\ 0 & 0 & 3 \\ \end{array}} \right)
- # Указать вдоль какого из векторов направлена главная ось тензора, имеющего в некотором ортонормированном базисе е1 следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} 1 & { - \sqrt 3 } & 0 \\ { - \sqrt 3 } & { - 1} & 0 \\ 0 & 0 & 3 \\ \end{array}} \right)
- # Указать вдоль какого из векторов направлена главная ось тензора, имеющего в некотором ортонормированном базисе е1 следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} 1 & { - \sqrt 3 } & 0 \\ { - \sqrt 3 } & { - 1} & 0 \\ 0 & 0 & 3 \\ \end{array}} \right)
- # Указать вдоль какого из векторов направлена главная ось тензора, имеющего в некотором ортонормированном базисе е1 следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} 1 & { - \sqrt 3 } & 0 \\ { - \sqrt 3 } & { - 1} & 0 \\ 0 & 0 & 2 \\ \end{array}} \right)
- # Указать вдоль какого из векторов направлена главная ось тензора, имеющего в некотором ортонормированном базисе е1 следующую матрицу компонент: \left( {\begin{array}{*{20}{c}} 1 & { - \sqrt 3 } & 0 \\ { - \sqrt 3 } & { - 1} & 0 \\ 0 & 0 & 2 \\ \end{array}} \right)
- # Базис ei образован единичными векторами, каждые два из которых образуют угол π/3. Укажите длину одного из векторов взаимного ему базиса.
- # Базис ei образован единичными векторами, каждые два из которых образуют угол π/3. Укажите длину одного из векторов взаимного ему базиса.
- # Базис ei образован единичными векторами, каждые два из которых образуют угол π/3. Укажите один из векторов взаимного ему базиса.
- # Диадные произведения базисных векторов представляют собой:
- # Результатом диадного произведения двух векторов будет:
- # Укажите несправедливое равенство для неопределенного умножения векторов:
- # Укажите определение симметричного тензора:
- # Укажите определение антисимметричного тензора:
- # Укажите выражение, справедливое для неопределенного умножения векторов:
- # Суммирование двух тензоров может выполняться в случае, если:
- # Вычитание двух тензоров может выполняться в случае, если:
- # Результатом сложения двух тензоров будет являться:
- # Градиент тензора - это ...
- # Оператор Гамильтона - это ...
- # Укажите физический смысл градиента скалярной функции векторного аргумента:
- # Укажите значение метрического коэффициента взаимного базиса g11 в декартовой системе координат:
- # Укажите значение метрического коэффициента взаимного базиса g22 в декартовой системе координат:
- # Укажите значение метрического коэффициента взаимного базиса g32 в декартовой системе координат:
- # Укажите значение метрического коэффициента взаимного базиса g11 в цилиндрической системе координат:
- # Укажите значение метрического коэффициента взаимного базиса g22 в цилиндрической системе координат:
- # Укажите значение метрического коэффициента взаимного базиса g23 в цилиндрической системе координат:
-
#
Выразите вектор
![math]() связанного с цилиндрической системой координат физического базиса
связанного с цилиндрической системой координат физического базиса ![math]() , через базисы
, через базисы ![math]() цилиндрической и
цилиндрической и ![math]() декартовой систем координат
декартовой систем координат
-
#
Выразите вектор
![math]() связанного с цилиндрической системой координат физического базиса
связанного с цилиндрической системой координат физического базиса ![math]() , через базисы
, через базисы ![math]() цилиндрической и
цилиндрической и ![math]() декартовой систем координат
декартовой систем координат
-
#
Выразите вектор
![math]() связанного с цилиндрической системой координат физического базиса
связанного с цилиндрической системой координат физического базиса ![math]() , через базисы
, через базисы ![math]() цилиндрической и
цилиндрической и ![math]() декартовой систем координат
декартовой систем координат
-
#
Какому из перечисленных ниже значений равна одна из контрвариантных компонент суммы тензоров
![math]() и
и ![math]() , где
, где ![math]() - базис системы координат
- базис системы координат ![math]() ,
, ![math]() ,
, ![math]() ,
, ![math]() и
и ![math]() - декартовы координаты
- декартовы координаты
-
#
Какому из перечисленных ниже значений равна одна из контрвариантных компонент суммы тензоров
![math]() и
и ![math]() , где
, где ![math]() - базис системы координат
- базис системы координат ![math]() ,
, ![math]() ,
, ![math]() ,
, ![math]() и
и ![math]() - декартовы координаты
- декартовы координаты
-
#
Какому из перечисленных ниже значений равна одна из контрвариантных компонент суммы тензоров
![math]() и
и ![math]() , где
, где ![math]() - базис системы координат
- базис системы координат ![math]() ,
, ![math]() ,
, ![math]() ,
, ![math]() и
и ![math]() - декартовы координаты
- декартовы координаты
-
#
Тело вращается вокруг оси с угловой скоростью
![math]() . Найдите физическую компоненту
. Найдите физическую компоненту ![math]() вектора угловой скорости в цилиндрической системе координат, для которой координатной линией
вектора угловой скорости в цилиндрической системе координат, для которой координатной линией ![math]() является ось вращения.
является ось вращения.
-
#
Тело вращается вокруг оси с угловой скоростью
![math]() . Найдите физическую компоненту
. Найдите физическую компоненту ![math]() вектора угловой скорости в цилиндрической системе координат, для которой координатной линией
вектора угловой скорости в цилиндрической системе координат, для которой координатной линией ![math]() является ось вращения.
является ось вращения.
-
#
Тело вращается вокруг оси с угловой скоростью
![math]() . Найдите физическую компоненту
. Найдите физическую компоненту ![math]() вектора угловой скорости в цилиндрической системе координат, для которой координатной линией
вектора угловой скорости в цилиндрической системе координат, для которой координатной линией ![math]() является ось вращения.
является ось вращения.
-
#
Верно ли утверждение, что если компонента
![math]() векторного поля в некоторой системе координат равна нулю во всех точках, то в этой системе координат и
векторного поля в некоторой системе координат равна нулю во всех точках, то в этой системе координат и ![math]() ?
?
- # Вычислите ковариантные производные компонент метрического тензора
- # Вычислите ковариантные производные компонент тензора Леви-Чивита
-
#
Тело вращается вокруг оси с угловой скоростью
![math]() . Найдите физическую компоненту
. Найдите физическую компоненту ![math]() вектора углового ускорения в цилиндрической системе координат, для которой координатной линией
вектора углового ускорения в цилиндрической системе координат, для которой координатной линией ![math]() является ось вращения.
является ось вращения.
-
#
Тело вращается вокруг оси с угловой скоростью
![math]() . Найдите физическую компоненту
. Найдите физическую компоненту ![math]() вектора углового ускорения в цилиндрической системе координат, для которой координатной линией
вектора углового ускорения в цилиндрической системе координат, для которой координатной линией ![math]() является ось вращения.
является ось вращения.
-
#
Тело вращается вокруг оси с угловой скоростью
![math]() . Найдите физическую компоненту
. Найдите физическую компоненту ![math]() вектора углового ускорения в цилиндрической системе координат, для которой координатной линией
вектора углового ускорения в цилиндрической системе координат, для которой координатной линией ![math]() является ось вращения.
является ось вращения.
-
#
Найдите символ Кристоффеля
![math]() для цилиндрической системы координат
для цилиндрической системы координат
-
#
Найдите символ Кристоффеля
![math]() для цилиндрической системы координат
для цилиндрической системы координат
-
#
Найдите символ Кристоффеля
![math]() для цилиндрической системы координат
для цилиндрической системы координат
- # Дивергенция тензора определяется как:
- # Укажите определение дивергенции вектора в точке векторного поля:
- # При определении дивергенции тензора:
- # Ротор тензора определяется как:
- # Укажите физический смысл ротора вектора скорости при вращении твердого тела относительно неподвижной оси:
- # При определении ротора тензора:
- # Укажите физический смысл дивергенции вектора скорости течения жидкости в точке поля:
- # Укажите физический смысл ротора вектора скорости течения жидкости в точке поля:
- # Укажите обозначение дивергенции функции F:
- # Укажите отличительную особенность псевдовектора:
- # Оператор Лапласа векторного поля эквивалентен:
- # Оператор Лапласа обозначается символом:
- # Определение теоремы Остроградского-Гаусса:
- # Определение теоремы Стокса:
- # Укажите обозначение ротора функции F:
- # Способ Эйлера для описания движения сплошной среды заключается:
- # Способ Лагранжа для описания движения сплошной среды заключается:
- # Способы Эйлера и Лагранжа для описания движения сплошной среды:
- # Движение среды происходит по закону: x1=1+a*t*2 x2=2+b*t*1 x3=3, где a,b=const. Найти составляющую поля скорости 1 в лагранжевом описании
- # Движение среды происходит по закону: x1=1+a*t*2 x2=2+b*t*1 x3=3, где a,b=const. Найти составляющую поля скорости 2 в лагранжевом описании
- # Движение среды происходит по закону: x1=1+a*t*2 x2=2+b*t*1 x3=3, где a,b=const. Найти составляющую поля скорости 3 в лагранжевом описании
-
#
Движение среды происходит по закону:
![math]() ,
, ![math]() ,
, ![math]() , где =const. Найти составляющую поля скорости 1 в лагранжевом описании
, где =const. Найти составляющую поля скорости 1 в лагранжевом описании
-
#
Движение среды происходит по закону:
![math]() ,
, ![math]() ,
, ![math]() , где =const. Найти составляющую поля скорости 2 в лагранжевом описании
, где =const. Найти составляющую поля скорости 2 в лагранжевом описании
-
#
Движение среды происходит по закону:
![math]() ,
, ![math]() ,
, ![math]() , где =const. Найти составляющую поля скорости 3 в лагранжевом описании
, где =const. Найти составляющую поля скорости 3 в лагранжевом описании
- # Движение среды происходит по закону: x1=1+a*t*2 x2=2+b*t*1 x3=3, где a,b=const. Найти лагранжеву координату 1 частицы, которая в момент t0 находится в точке пространства с координатами (x01,x02,x03)
- # Движение среды происходит по закону: x1=1+a*t*2 x2=2+b*t*1 x3=3, где a,b=const. Найти лагранжеву координату 2 частицы, которая в момент t0 находится в точке пространства с координатами (x01,x02,x03)
- # Движение среды происходит по закону: x1=1+a*t*2 x2=2+b*t*1 x3=3, где a,b=const. Найти лагранжеву координату 3 частицы, которая в момент t0 находится в точке пространства с координатами (x01,x02,x03)
-
#
Движение среды происходит по закону:
![math]() ,
, ![math]() ,
, ![math]() , где =const. Найти составляющую поля ускорения а1 в лагранжевом описании
, где =const. Найти составляющую поля ускорения а1 в лагранжевом описании
-
#
Движение среды происходит по закону:
![math]() ,
, ![math]() ,
, ![math]() , где =const. Найти составляющую поля ускорения а2 в лагранжевом описании
, где =const. Найти составляющую поля ускорения а2 в лагранжевом описании
-
#
Движение среды происходит по закону:
![math]() ,
, ![math]() ,
, ![math]() , где =const. Найти составляющую поля ускорения а3 в лагранжевом описании
, где =const. Найти составляющую поля ускорения а3 в лагранжевом описании
-
#
Найти составляющую поля ускорения а1 движения среды, если оно происходит с полем скорости
![math]() ,
, ![math]() ,
, ![math]() , где =const > 0
, где =const > 0
-
#
Найти составляющую поля ускорения а2 движения среды, если оно происходит с полем скорости
![math]() ,
, ![math]() ,
, ![math]() , где =const > 0
, где =const > 0
-
#
Найти составляющую поля ускорения а3 движения среды, если оно происходит с полем скорости
![math]() ,
, ![math]() ,
, ![math]() , где =const > 0
, где =const > 0
-
#
Движение среды происходит по закону:
![math]() ,
, ![math]() ,
, ![math]() , где =const. Укажите координату x1 частицы в момент t=3*, которая в момент t= находилась в точке пространства с координатами (a,b,c)
, где =const. Укажите координату x1 частицы в момент t=3*, которая в момент t= находилась в точке пространства с координатами (a,b,c)
-
#
Движение среды происходит по закону:
![math]() ,
, ![math]() ,
, ![math]() , где =const. Укажите координату x2 частицы в момент t=3*T, которая в момент t=T находилась в точке пространства с координатами (a,b,c)
, где =const. Укажите координату x2 частицы в момент t=3*T, которая в момент t=T находилась в точке пространства с координатами (a,b,c)
-
#
Движение среды происходит по закону:
![math]() ,
, ![math]() ,
, ![math]() , где =const. Укажите координату x3 частицы в момент t=3*, которая в момент t= находилась в точке пространства с координатами (a,b,c)
, где =const. Укажите координату x3 частицы в момент t=3*, которая в момент t= находилась в точке пространства с координатами (a,b,c)
 тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат  для течений среды с полями скорости, имеющими в этих координатах компоненты:
для течений среды с полями скорости, имеющими в этих координатах компоненты:  ,
, ,
, , где
, где 
 тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат  девиатора тензора скоростей деформаций
девиатора тензора скоростей деформаций  в пространственной декартовой системе координат
в пространственной декартовой системе координат  девиатора тензора скоростей деформаций
девиатора тензора скоростей деформаций  девиатора тензора скоростей деформаций
девиатора тензора скоростей деформаций  ,
, , где
, где 
 тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат  ,
, ,
, тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат  тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат  тензора скоростей деформаций в пространственной декартовой системе координат
тензора скоростей деформаций в пространственной декартовой системе координат  ,
,
 ,
, ,
, , найти компоненту
, найти компоненту  вектора
вектора 
 вектора
вектора  вектора
вектора  ,
, ,
, ,
, Определить главный компонент
Определить главный компонент  тензора напряжений
тензора напряжений  тензора напряжений
тензора напряжений  тензора напряжений
тензора напряжений 


 между
между 

 ,
, . Здесь значения
. Здесь значения  отнесены к некоторому характерному значению напряжения
отнесены к некоторому характерному значению напряжения  и приведены в безразмерном виде. Определить главный компонент
и приведены в безразмерном виде. Определить главный компонент  необходимо из-за наличия поверхностного натяжения совершить работу
необходимо из-за наличия поверхностного натяжения совершить работу  , где
, где  — коэффициент поверхностного натяжения. Какую работу необходимо затратить, чтобы разделить 1 л воды на капли диаметром 0,01 мм? Принять, что
— коэффициент поверхностного натяжения. Какую работу необходимо затратить, чтобы разделить 1 л воды на капли диаметром 0,01 мм? Принять, что 
 , коэффициент Пуассона
, коэффициент Пуассона  , удельная теплоемкость при постоянных деформациях
, удельная теплоемкость при постоянных деформациях  , коэффициент линейного теплового расширения
, коэффициент линейного теплового расширения  . Модуль Юнга и коэффициент Пуассона выражаются через коэффициенты Ламе по формулам:
. Модуль Юнга и коэффициент Пуассона выражаются через коэффициенты Ламе по формулам:  ,
,
 -вектор скорости,
-вектор скорости,  -потенциал скорости):
-потенциал скорости):  расход жидкости
расход жидкости 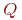 через криволинейную дугу, соединяющую точки с координатами
через криволинейную дугу, соединяющую точки с координатами  и
и 

 выразить физическую компоненту скорости
выразить физическую компоненту скорости  в правой ортогональной криволинейной системе координат
в правой ортогональной криволинейной системе координат  , где
, где  — координаты в плоскости меридиана,
— координаты в плоскости меридиана,  — угол, определяющий положение плоскости меридиана.
— угол, определяющий положение плоскости меридиана.  - параметры Ламе
- параметры Ламе  в правой ортогональной криволинейной системе координат
в правой ортогональной криволинейной системе координат 

 в цилиндрической системе координат
в цилиндрической системе координат 
 в цилиндрической системе координат
в цилиндрической системе координат 
 в сферической системе координат
в сферической системе координат 
 в сферической системе координат
в сферической системе координат  , имеющего в некотором ортонормированном базисе еi следующую матрицу компонент:
\left( {\begin{array}{*{20}{c}}
1 & { - \sqrt 3 } & 0 \\
{ - \sqrt 3 } & { - 1} & 0 \\
0 & 0 & 3 \\
\end{array}} \right)
, имеющего в некотором ортонормированном базисе еi следующую матрицу компонент:
\left( {\begin{array}{*{20}{c}}
1 & { - \sqrt 3 } & 0 \\
{ - \sqrt 3 } & { - 1} & 0 \\
0 & 0 & 3 \\
\end{array}} \right)  связанного с цилиндрической системой координат физического базиса
связанного с цилиндрической системой координат физического базиса  , через базисы
, через базисы  цилиндрической и
цилиндрической и  декартовой систем координат
декартовой систем координат  связанного с цилиндрической системой координат физического базиса
связанного с цилиндрической системой координат физического базиса  связанного с цилиндрической системой координат физического базиса
связанного с цилиндрической системой координат физического базиса  и
и  , где
, где  ,
,  ,
,  ,
,  и
и  - декартовы координаты
- декартовы координаты  . Найдите физическую компоненту
. Найдите физическую компоненту  вектора угловой скорости в цилиндрической системе координат, для которой координатной линией
вектора угловой скорости в цилиндрической системе координат, для которой координатной линией  является ось вращения.
является ось вращения.  вектора угловой скорости в цилиндрической системе координат, для которой координатной линией
вектора угловой скорости в цилиндрической системе координат, для которой координатной линией  вектора угловой скорости в цилиндрической системе координат, для которой координатной линией
вектора угловой скорости в цилиндрической системе координат, для которой координатной линией  векторного поля в некоторой системе координат равна нулю во всех точках, то в этой системе координат и
векторного поля в некоторой системе координат равна нулю во всех точках, то в этой системе координат и  ?
?  вектора углового ускорения в цилиндрической системе координат, для которой координатной линией
вектора углового ускорения в цилиндрической системе координат, для которой координатной линией  вектора углового ускорения в цилиндрической системе координат, для которой координатной линией
вектора углового ускорения в цилиндрической системе координат, для которой координатной линией  вектора углового ускорения в цилиндрической системе координат, для которой координатной линией
вектора углового ускорения в цилиндрической системе координат, для которой координатной линией  для цилиндрической системы координат
для цилиндрической системы координат  для цилиндрической системы координат
для цилиндрической системы координат  для цилиндрической системы координат
для цилиндрической системы координат  ,
,  ,
,  , где =const. Найти составляющую поля скорости 1 в лагранжевом описании
, где =const. Найти составляющую поля скорости 1 в лагранжевом описании  ,
,  ,
,  , где =const > 0
, где =const > 0