Главная /
Введение в теорию множеств и комбинаторику
Введение в теорию множеств и комбинаторику - ответы на тесты Интуит
Приводятся начальные сведения о множествах и основные понятия подмножества, мощности, булеана. Даются возможные способы представления множеств и рассматриваются операции над множествами, такие как объединение, пересечение, разность, симметрическая разность и дополнение.
Список вопросов:
-
#
Какие из приведенных множеств заданы верно?
![math]() ,
, ![math]() ,
, ![math]() - множество цифр (арабских).
- множество цифр (арабских).
-
#
Корректно ли описаны конечные множества?
![math]() ,
, ![math]() ,
, ![math]() - множество цифр (арабских),
- множество цифр (арабских), ![math]() - множество чисел.
- множество чисел.
-
#
Правильно ли представлены следующие множества?
![math]() ,
, ![math]() ,
, ![math]() - множество цифр (арабских),
- множество цифр (арабских), ![math]() - множество чисел.
- множество чисел.
-
#
Даны множества
![math]() и
и ![math]() .
Найти мощности этих множеств. Является ли множество
.
Найти мощности этих множеств. Является ли множество ![math]() подмножеством множества
подмножеством множества ![math]() ?
?
-
#
Даны множества
![math]() и
и ![math]() . Равны ли они?
Записать элементы множества
. Равны ли они?
Записать элементы множества ![math]() , равного множествам
, равного множествам ![math]() и
и ![math]() .
Сколько вариантов записи множества
.
Сколько вариантов записи множества ![math]() существует?
существует?
-
#
Даны множества
![math]() и
и ![math]() .
Найти мощности этих множеств. Является ли множество
.
Найти мощности этих множеств. Является ли множество ![math]() собственным подмножеством множества
собственным подмножеством множества ![math]() ?
?
-
#
К какому типу относятся следующие множества? Представить элементы множеств в явном виде, если это возможно, и подсчитать мощность множеств.
![math]() - множество цифр, например, арабских.
- множество цифр, например, арабских.![math]() - множество целых положительных четных чисел.
- множество целых положительных четных чисел.![math]() - множество двузначных чисел, являющихся степенями 2, которые нацело делятся на 5.
- множество двузначных чисел, являющихся степенями 2, которые нацело делятся на 5.
-
#
К какому типу относятся следующие множества? Представить элементы множеств в явном виде, если это возможно, и подсчитать мощность множеств.
![math]() - множество гласных букв русского алфавита.
- множество гласных букв русского алфавита.![math]() - множество целых положительных нечетных чисел.
- множество целых положительных нечетных чисел.![math]() - множество двузначных чисел, являющихся степенями 2.
- множество двузначных чисел, являющихся степенями 2.
-
#
К какому типу относятся следующие множества? Представить элементы множеств в явном виде, если это возможно, и подсчитать мощность множеств.
![math]() - множество нечетных чисел, больших 3 и меньших 10.
- множество нечетных чисел, больших 3 и меньших 10. ![math]() - множество целых положительных четных чисел.
- множество целых положительных четных чисел.![math]() - множество трехзначных чисел, являющихся степенями 2, которые нацело делятся на 5.
- множество трехзначных чисел, являющихся степенями 2, которые нацело делятся на 5.
-
#
Заданы универсальное множество
![math]() и множества
и множества ![math]() ,
, ![math]() и
и ![math]() на рисунке. Записать элементы множеств
на рисунке. Записать элементы множеств ![math]() ,
, ![math]() и
и ![math]() .
[Большая Картинка]
.
[Большая Картинка]
-
#
Заданы универсальное множество
![math]() и множества
и множества ![math]() ,
, ![math]() и
и ![math]() .
Представить эти множества графически.
.
Представить эти множества графически.
-
#
Заданы универсальное множество
![math]() и множества
и множества ![math]() ,
, ![math]() и
и ![math]() на рисунке. Записать элементы множеств
на рисунке. Записать элементы множеств ![math]() ,
, ![math]() и
и ![math]() .
[Большая Картинка]
.
[Большая Картинка]
-
#
Дано множество
![math]() . Составить булеан множества и определить его мощность.
. Составить булеан множества и определить его мощность.
-
#
Дано множество
![math]() . Составить булеан множества и определить его мощность.
. Составить булеан множества и определить его мощность.
-
#
Дано множество
![math]() . Составить булеан множества и определить его мощность.
. Составить булеан множества и определить его мощность.
-
#
Заданы множества
![math]() . Найти множества:
. Найти множества:
![math]()
-
#
Заданы множества
![math]() . Найти множества:
. Найти множества:
![math]()
-
#
Заданы множества
![math]() . Найти множества:
. Найти множества:
![math]()
-
#
Заданы множества
![math]() . Найти множества:
. Найти множества:
![math]()
-
#
Пусть множество
![math]() включает в себя корни уравнения
включает в себя корни уравнения ![math]() , а множество
, а множество ![math]() содержит значения
содержит значения ![math]() . Найти элементы множества
. Найти элементы множества ![math]() .
.
-
#
Пусть множество
![math]() включает в себя корни уравнения
включает в себя корни уравнения ![math]() , а множество
, а множество ![math]() содержит значения
содержит значения ![math]() . Найти элементы множества
. Найти элементы множества ![math]() .
.
-
#
Пусть множество
![math]() включает в себя корни уравнения
включает в себя корни уравнения ![math]() , а множество
, а множество ![math]() содержит значения
содержит значения ![math]() . Найти элементы множества
. Найти элементы множества ![math]() .
.
-
#
Заданы множества
![math]() . Найти множество:
. Найти множество: ![math]()
-
#
Заданы множества
![math]() . Найти множество:
. Найти множество: ![math]()
-
#
Заданы множества
![math]() . Найти множество:
. Найти множество: ![math]()
-
#
Заданы множества
![math]() . Найти множество
. Найти множество ![math]()
-
#
Заданы множества
![math]() . Найти множество
. Найти множество ![math]()
-
#
Пусть E = \left\{ {1, 2, 3, 4, 5} \right\}, X = \left\{ {1, 5} \right\}, Y = \left\{ {1, 2, 4} \right\}, Z =
\left\{ {2, 5} \right\}. Найти множество и дать графическую интерпретацию операциям:
![math]()
-
#
Пусть
![math]() . Найти множество:
. Найти множество: ![math]()
-
#
Пусть
![math]() . Чему равно множество
. Чему равно множество ![math]()
-
#
Выполняется ли соотношение
![math]() ?
?
-
#
Верно ли на рисунке представлено графическое доказательство соотношения
![math]() ?
[Большая Картинка]
[Большая Картинка]
?
[Большая Картинка]
[Большая Картинка]
-
#
Верно ли на рисунке представлено графическое доказательство соотношения
![math]() ?
[Большая Картинка]
[Большая Картинка]
?
[Большая Картинка]
[Большая Картинка]
-
#
Выполняется ли соотношение
![math]() ?
?
-
#
Выполняется ли соотношение
![math]() ?
?
-
#
Верно ли на рисунке представлено графическое доказательство соотношения
![math]() ?
[Большая Картинка]
[Большая Картинка]
?
[Большая Картинка]
[Большая Картинка]
-
#
Выполняется ли соотношение
![math]() ?
?
-
#
Найти множество, выполнив предварительные преобразования и используя законы алгебры множеств: (
![math]() )
)
-
#
Упростить выражение : (
![math]() )
)
-
#
Упростить выражение
![math]()
-
#
Выполнить преобразования выражения
![math]()
- # В классе 35 учащихся. Из них 20 посещают математический кружок, 11 - физический, 10 учащихся не посещают ни одного из этих кружков: сколько учеников посещают и математический и физический кружок?
- # В классе 35 учащихся. Из них 20 посещают математический кружок, 11 - физический, 10 учащихся не посещают ни одного из этих кружков: сколько учащихся посещают только математический кружок?
- # В классе 35 учащихся. Из них 20 посещают математический кружок, 11 - физический, 10 учащихся не посещают ни одного из этих кружков: сколько учащихся посещают только физический кружок?
- # Найти число целых положительных чисел, не превосходящих 300 и не делящихся ни на одно из чисел 2, 3 и 5.
- # Найти число целых положительных чисел, не превосходящих 200 и не делящихся ни на одно из чисел 2, 3 и 5.
- # Найти число целых положительных чисел, не превосходящих 300 и делящихся хотя бы на одно из чисел 2, 3 и 5.
- # Найти число целых положительных чисел, не превосходящих 300 и делящихся и на 2, и на 3 и на 5.
- # По результатам опроса студенческой группы из 32 человек 12 регулярно читают журнал "Мир ПК", 10 человек читают журнал "Открытые системы", 8 человек предпочитают журнал "Знание-сила", 3 человека читают и "Мир ПК" и "Открытые системы", 4 человека читают "Мир ПК" и "Знание-сила", 5 человек - "Открытые системы" и "Знание-сила", а 1 человек читает все три журнала. Сколько человек читают только "Мир ПК" ?
- # По результатам опроса студенческой группы из 32 человек 12 регулярно читают журнал "Мир ПК", 10 человек читают журнал "Открытые системы", 8 человек предпочитают журнал "Знание-сила", 3 человека читают и "Мир ПК" и "Открытые системы", 4 человека читают "Мир ПК" и "Знание-сила", 5 человек - "Открытые системы" и "Знание-сила", а 1 человек читает все три журнала. Сколько человек читают только "Открытые системы"?
- # По результатам опроса студенческой группы из 32 человек 12 регулярно читают журнал "Мир ПК", 10 человек читают журнал "Открытые системы", 8 человек предпочитают журнал "Знание-сила", 3 человека читают и "Мир ПК" и "Открытые системы", 4 человека читают "Мир ПК" и "Знание-сила", 5 человек - "Открытые системы" и "Знание-сила", а 1 человек читает все три журнала. Сколько человек читают только "Знание-сила" ?
- # По результатам опроса студенческой группы из 32 человек 12 регулярно читают журнал "Мир ПК", 10 человек читают журнал "Открытые системы", 8 человек предпочитают журнал "Знание-сила", 3 человека читают и "Мир ПК" и "Открытые системы", 4 человека читают "Мир ПК" и "Знание-сила", 5 человек - "Открытые системы" и "Знание-сила", а 1 человек читает все три журнала. Сколько человек читают ровно два из названных журналов ?
-
#
Даны множества
![math]() . Найти прямое произведение
. Найти прямое произведение ![math]() .
.
-
#
Дано множество
![math]() . Найти прямое произведение
. Найти прямое произведение ![math]() .
.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Записать отношение в явном виде.
. Записать отношение в явном виде.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() .Записать отношение в явном виде.
.Записать отношение в явном виде.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Записать отношение в явном виде .
. Записать отношение в явном виде .
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Выписать все элементы
. Выписать все элементы ![math]() и
и ![math]() .
.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Выписать все элементы
. Выписать все элементы ![math]() и
и ![math]() .
.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Выписать все элементы
. Выписать все элементы ![math]() и
и ![math]() .
.
-
#
Дано множество
![math]() . Найти тождественное и универсальное множества.
. Найти тождественное и универсальное множества.
-
#
Дано множество
![math]() . Найти тождественное и универсальное множества.
. Найти тождественное и универсальное множества.
-
#
Дано множество
![math]() . Найти тождественное и универсальное множества.
. Найти тождественное и универсальное множества.
-
#
Даны множества
![math]() и
и ![math]() . a) записать элементы множества
. a) записать элементы множества ![math]() в явном виде, если
в явном виде, если ![math]() . б). записать элементы отношения
. б). записать элементы отношения ![math]() ; в). найти область определения
; в). найти область определения ![math]() и область значений
и область значений ![math]() .
.
-
#
Даны множества
![math]() и
и ![math]() . a) записать элементы множества
. a) записать элементы множества ![math]() в явном виде, если
в явном виде, если ![math]() . б). записать элементы отношения
. б). записать элементы отношения ![math]() ; в). найти область определения
; в). найти область определения ![math]() и область значений
и область значений ![math]() .
.
-
#
Даны множества
![math]() и
и ![math]() . a) записать элементы множества
. a) записать элементы множества ![math]() в явном виде, если
в явном виде, если ![math]() . б). записать элементы отношения
. б). записать элементы отношения ![math]() ; в). найти область определения
; в). найти область определения ![math]() и область значений
и область значений ![math]() .
.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() \rho = \left\{ {(-3, -3), (-3, -1), (-3, 1), (-3, 3),
(-1, -1), (-1, 1), (3, -3), (-1, -3), (1, -3), (1, -1)} \right\}. Каким способом представлено отношение на рисунке:
[Большая Картинка]
\rho = \left\{ {(-3, -3), (-3, -1), (-3, 1), (-3, 3),
(-1, -1), (-1, 1), (3, -3), (-1, -3), (1, -3), (1, -1)} \right\}. Каким способом представлено отношение на рисунке:
[Большая Картинка]
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() \rho = \left\{ {(-3, -3), (-3, -1), (-3, 1), (-3, 3),
(-1, -1), (-1, 1), (3, -3), (-1, -3), (1, -3), (1, -1)} \right\}. Каким способом представлено отношение на рисунке:
[Большая Картинка]
\rho = \left\{ {(-3, -3), (-3, -1), (-3, 1), (-3, 3),
(-1, -1), (-1, 1), (3, -3), (-1, -3), (1, -3), (1, -1)} \right\}. Каким способом представлено отношение на рисунке:
[Большая Картинка]
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]()
![math]() . Каким способом представлено отношение на рисунке:
[Большая Картинка]
. Каким способом представлено отношение на рисунке:
[Большая Картинка]
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Выписать все элементы
. Выписать все элементы ![math]() и представить
и представить ![math]() линейным способом.
[Большая Картинка]
[Большая Картинка]
[Большая Картинка]
линейным способом.
[Большая Картинка]
[Большая Картинка]
[Большая Картинка]
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Выписать все элементы
. Выписать все элементы ![math]() и представить
и представить ![math]() линейным способом.
[Большая Картинка]
[Большая Картинка]
[Большая Картинка]
линейным способом.
[Большая Картинка]
[Большая Картинка]
[Большая Картинка]
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Выписать все элементы
. Выписать все элементы ![math]() и представить
и представить ![math]() координатным способом.
[Большая Картинка]
[Большая Картинка]
[Большая Картинка]
координатным способом.
[Большая Картинка]
[Большая Картинка]
[Большая Картинка]
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() : a) записать отношение в явном виде; б)определить свойства отношения
: a) записать отношение в явном виде; б)определить свойства отношения ![math]() .
.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() : a) записать отношение в явном виде; б)определить свойства отношения
: a) записать отношение в явном виде; б)определить свойства отношения ![math]() .
.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() : a) записать отношение в явном виде; б)определить свойства отношения
: a) записать отношение в явном виде; б)определить свойства отношения ![math]() .
.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() : a) записать отношение в явном виде; б) определить свойства отношения
: a) записать отношение в явном виде; б) определить свойства отношения ![math]() .
.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() : a) записать отношение в явном виде; б) определить свойства отношения
: a) записать отношение в явном виде; б) определить свойства отношения ![math]() .
.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() : a) записать отношение в явном виде; б) определить свойства отношения
: a) записать отношение в явном виде; б) определить свойства отношения ![math]() .
.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.
-
#
Пусть имеется отношение
![math]() . Обладает ли данное отношение свойством эквивалентности?
. Обладает ли данное отношение свойством эквивалентности?
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() .Записать отношение в явном виде. Обладает ли данное отношение свойством эквивалентности?
.Записать отношение в явном виде. Обладает ли данное отношение свойством эквивалентности?
-
#
Пусть имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Обладает ли данное отношение свойством эквивалентности?
. Обладает ли данное отношение свойством эквивалентности?
-
#
Дано отношение
![math]() . Является ли оно функцией?
. Является ли оно функцией?
-
#
Имеется множество
![math]() и задано отношение
и задано отношение ![math]() . Является ли оно функцией?
. Является ли оно функцией?
-
#
Дано множество
![math]() и задано отношение
и задано отношение ![math]() : a) является ли оно функцией? б) является ли оно отображением?
: a) является ли оно функцией? б) является ли оно отображением?
- # Сколько трехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5?
- # Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5?
- # Сколько трехзначных нечетных чисел можно составить из цифр 0, 1, 2, 3, 4, 5?
- # Сколько пятизначных чисел, у которых все цифры нечетные?
- # Сколько трехзначных чисел, у которых все цифры нечетные?
- # Сколько пятизначных чисел, у которых все цифры четные?
- # Сколько имеется пятизначных чисел, которые делятся на 5?
- # Сколько имеется четырехзначных чисел, которые делятся на 5?
- # Сколько имеется пятизначных чисел, которые делятся на 5?
- # Сколько пятизначных чисел, которые одинаково читаются слева направо и справа налево (например, 67876,17071)?
- # Сколько трехзначных чисел, которые одинаково читаются слева направо и справа налево (например, 67876,17071)?
- # Сколько пятизначных чисел, которые одинаково читаются слева направо и справа налево (например, 67876 или 17071)?
-
#
Сколькими способами можно составить предложение, переставляя 3 слова: "мама" "мыла" "раму"?
Решение. Перестановки трех различных слов можно получить
![math]() способами, т. е. всего вариантов . . . . .
способами, т. е. всего вариантов . . . . .
-
#
Сколькими способами можно составить предложение, переставляя 3 слова: "кот" "сметану" "съел"?
Решение. Перестановки трех различных слов можно получить
![math]() способами, т. е. всего вариантов . . . . .
способами, т. е. всего вариантов . . . . .
- # Сколькими способами можно составить предложение, переставляя 4 слова: "студент" "экзамен" "сдал" "хорошо"?
- # Сколько различных слов можно составить, переставляя буквы слова "комбинаторика"?
- # Сколько различных слов можно составить, переставляя буквы слова "знание"?
- # Сколько различных слов можно составить, переставляя буквы слова "банан"?
- # Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие 2 лица одного пола не сидели рядом?
- # Сколькими способами можно посадить за круглый стол 3 мужчин и 3 женщин так, чтобы никакие 2 лица одного пола не сидели рядом?
- # Сколькими способами можно посадить за круглый стол 4 мужчин и 4 женщин так, чтобы никакие 2 лица одного пола не сидели рядом?
- # Сколькими способами можно посадить 4 мужчин и 4 женщин так, чтобы никакие 2 лица одного пола не сидели рядом на карусели и способы, переходящие друг в друга при вращении карусели, считаются совпадающими?
- # Сколькими способами можно посадить 5 мужчин и 5 женщин так, чтобы никакие 2 лица одного пола не сидели рядом на карусели и способы, переходящие друг в друга при вращении карусели, считаются совпадающими?
- # Сколькими способами можно посадить 3 мужчин и 3 женщин так, чтобы никакие 2 лица одного пола не сидели рядом на карусели и способы, переходящие друг в друга при вращении карусели, считаются совпадающими?
- # Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов? [Большая Картинка]
- # Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов при условии, что одна из полос должна быть красной? [Большая Картинка]
- # Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 6 различных цветов? [Большая Картинка]
- # На железнодорожной станции имеется m светофоров. Сколько может быть дано различных сигналов, если каждый светофор имеет 3 состояния: красный, желтый и зеленый? [Большая Картинка]
- # На железнодорожной станции имеется 5 светофоров. Сколько может быть дано различных сигналов, если каждый светофор имеет 3 состояния: красный, желтый и зеленый? [Большая Картинка]
- # На железнодорожной станции имеется 4 светофора. Сколько может быть дано различных сигналов, если каждый светофор имеет 3 состояния: красный, желтый и зеленый? [Большая Картинка]
- # Сколькими способами можно выбрать 3 различные краски из имеющихся 5?
- # Сколькими способами можно выбрать 4 различные краски из имеющихся 6?
- # Сколькими способами можно выбрать 5 различных красок из имеющихся 6?
- # Сколькими способами можно выбрать три пирожных из 6 различных сортов?
- # Сколькими способами можно выбрать 8 пирожных из имеющихся в наличии 6 различных сортов?
- # Сколькими способами можно выбрать 5 пирожных из имеющихся в наличии 3 различных сортов?
- # У мамы 2 яблока и 3 груши. Каждый день в течении 5 дней подряд она выдаёт по одному фрукту. Сколькими способами это может быть сделано?
- # У мамы 4 яблока и 3 груши. Каждый день в течении 5 дней подряд она выдаёт по одному фрукту. Сколькими способами это может быть сделано?
- # У мамы 5 яблок и 3 груши. Каждый день в течении 5 дней подряд она выдаёт по одному фрукту. Сколькими способами это может быть сделано?
- # В продаже имеется 3 гуся, 4 курицы и 2 утки. Сколькими способами можно сделать покупку, включающую все три вида птиц?
- # В продаже имеется 4 гуся, 3 курицы и 3 утки. Сколькими способами можно сделать покупку, включающую все три вида птиц?
- # В продаже имеется 4 гуся, 2 курицы и 4 утки. Сколькими способами можно сделать покупку, включающую все три вида птиц?
- # В магазине имеется 70 музыкальных CD дисков и 40 дисков с фильмами. Можно купить 2 музыкальных диска или 3 диска с фильмами. В каком случае при покупке больше вариантов выбора?
- # В магазине имеется 60 музыкальных CD дисков и 30 дисков с фильмами. Можно купить 2 музыкальных диска или 3 диска с фильмами. В каком случае при покупке больше вариантов выбора?
- # В магазине имеется 80 музыкальных CD дисков и 30 дисков с фильмами. Можно купить 2 музыкальных диска или 3 диска с фильмами. В каком случае при покупке больше вариантов выбора?
- # В группе 27 человек. Необходимо сформировать команду из 4 человек. Сколькими способами это можно сделать?
- # В группе 25 человек. Необходимо сформировать команду из 3 человек. Сколькими способами это можно сделать?
- # В группе 22 человека. Необходимо сформировать команду из 5 человек. Сколькими способами это можно сделать?
- # Из 3 различных экземпляров учебника алгебры, 7 экземпляров учебника геометрии и 7 экземпляров учебника тригонометрии надо выбрать по одному экземпляру каждого учебника. Сколькими способами это можно сделать?
- # Из 5 различных экземпляров учебника алгебры, 4 экземпляров учебника геометрии и 6 экземпляров учебника тригонометрии надо выбрать по одному экземпляру каждого учебника. Сколькими способами это можно сделать?
- # Из 8 различных экземпляров учебника алгебры, 3 экземпляров учебника геометрии и 5 экземпляров учебника тригонометрии надо выбрать по одному экземпляру каждого учебника. Сколькими способами это можно сделать?
- # В букинистическом магазине лежат 6 экземпляров романа И.С. Тургенева "Рудин", 3 экземпляра его же романа "Дворянское гнездо" и 4 экземпляра романа "Отцы и дети". Кроме того, есть 5 томов, содержащих романы "Рудин" и "Дворянское гнездо", и 7 томов, содержащих романы "Дворянское гнездо" и "Отцы и дети". Сколькими способами можно сделать покупку, содержащую по 1 экземпляру каждого из этих романов?
- # В букинистическом магазине лежат 5 экземпляров романа И.С. Тургенева "Рудин", 3 экземпляра его же романа "Дворянское гнездо" и 2 экземпляра романа "Отцы и дети". Кроме того, есть 4 томов, содержащих романы "Рудин" и "Дворянское гнездо", и 7 томов, содержащих романы "Дворянское гнездо" и "Отцы и дети". Сколькими способами можно сделать покупку, содержащую по 1 экземпляру каждого из этих романов?
- # В букинистическом магазине лежат 5 экземпляров романа И.С. Тургенева "Рудин" , 4 экземпляра его же романа "Дворянское гнездо" и 2 экземпляра романа "Отцы и дети". Кроме того, есть 5 томов, содержащих романы "Рудин" и "Отцы и дети", и 6 томов, содержащих романы "Дворянское гнездо" и "Отцы и дети". Сколькими способами можно сделать покупку, содержащую по 1 экземпляру каждого из этих романов?
- # В букинистическом магазине лежат 6 экземпляров романа И.С. Тургенева "Рудин" , 3 экземпляра его же романа "Дворянское гнездо" и 4 экземпляра романа "Отцы и дети". Кроме того, есть 5 томов, содержащих романы "Рудин" и "Дворянское гнездо", и 7 томов, содержащих романы "Дворянское гнездо" и "Отцы и дети", кроме того, в магазине есть 3 тома, в которые входят "Рудин" и "Отцы и дети". Сколькими способами можно сделать покупку, содержащую по 1 экземпляру каждого из этих романов?
- # В букинистическом магазине лежат 5 экземпляров романа И.С. Тургенева "Рудин" , 4 экземпляра его же романа "Дворянское гнездо" и 2 экземпляра романа " Отцы и дети". Кроме того, есть 6 томов, содержащих романы "Рудин" и "Дворянское гнездо", и 5 томов, содержащих романы "Дворянское гнездо" и "Отцы и дети", кроме того, в магазине есть 3 тома, в которые входят "Рудин" и "Отцы и дети". Сколькими способами можно сделать покупку, содержащую по 1 экземпляру каждого из этих романов?
- # В букинистическом магазине лежат 7 экземпляров романа И.С. Тургенева "Рудин" , 2 экземпляра его же романа "Дворянское гнездо" и 3 экземпляра романа "Отцы и дети". Кроме того, есть 4 тома, содержащих романы "Рудин" и "Дворянское гнездо", и 5 томов, содержащих романы "Дворянское гнездо" и "Отцы и дети", кроме того, в магазине есть 3 тома, в которые входят "Рудин" и "Отцы и дети". Сколькими способами можно сделать покупку, содержащую по 1 экземпляру каждого из этих романов?
- # По результатам опроса студенческой группы из 32 человек 12 человек регулярно читает журнал "Мир ПК", 10 человек читают журнал "Открытые системы", 8 человек предпочитают журнал "Знание-сила", 3 человека читают и "Мир ПК" и "Открытые системы", 4 человека читают "Мир ПК" и "Знание-сила", 5 человек - "Открытые системы" и "Знание-сила", а 1 человек читает все три журнала. Сколько человек не читает ни одного из перечисленных журналов?
- # По результатам опроса студенческой группы из 32 человек 10 человек регулярно читает журнал "Мир ПК", 13 человек читают журнал "Открытые системы", 12 человек предпочитают журнал "Знание-сила", 5 человек читают и "Мир ПК" и "Открытые системы", 3 человека читают "Мир ПК" и "Знание-сила", 6 человек - Открытые системы" и "Знание-сила", а 1 человек читает все три журнала. Сколько человек не читает ни одного из перечисленных журналов?
- # По результатам опроса студенческой группы из 32 человек 18 человек регулярно читает журнал "Мир ПК", 19 человек читают журнал "Открытые системы", 15 человек предпочитают журнал "Знание-сила", 8 человек читают и "Мир ПК" и "Открытые системы", 9 человек читают "Мир ПК" и "Знание-сила", 7 человек - "Открытые системы" и "Знание-сила", а 3 человека читает все три журнала. Сколько человек не читает ни одного из перечисленных журналов?
- # На потоке обучалось 65 студентов, все они посещали дисциплины по выбору, такие как "Теория графов", "Теория вероятности" и "Математическая статистика". Во время сессии "Теорию графов" успешно сдало 35 человек ; "Теорию вероятности" - 24 человека ; "Математическую статистику" - 22 чел. 8 - человек сдали "Теорию графов" и "Теорию вероятности", 7 человек - "Теорию графов" и "Мат. статистику", а 6 человек сдали "Теорию вероятности" и "Мат. статистику". 2 человека изучали все три дисциплины и успешно их сдали. Сколько человек не сдали экзамена ни по одной из перечисленных дисциплин?
- # На потоке обучалось 65 студентов, все они посещали дисциплины по выбору, такие как "Теория графов", "Теория вероятности" и "Математическая статистика". Во время сессии "Теорию графов" успешно сдало 32 человека; "Теорию вероятности" - 29 человек; "Математическую статистику" - 23 чел. 8 - человек сдали "Теорию графов" и "Теорию вероятности", 7 человек - "Теорию графов" и "Мат. статистику", а 9 человек сдали "Теорию вероятности" и "Мат. статистику". 3 человека изучали все три дисциплины и успешно их сдали. Сколько человек не сдали экзамена ни по одной из перечисленных дисциплин?
- # На потоке обучалось 65 студентов, все они посещали дисциплины по выбору, такие как "Теория графов", "Теория вероятности" и "Математическая статистика". Во время сессии "Теорию графов" успешно сдали 31 человек ; "Теорию вероятности" - 27 человек ; "Математическую статистику" - 25 чел. 9 человек сдали "Теорию графов" и "Теорию вероятности", 8 человек - "Теорию графов" и "Мат. статистику", а 7 человек сдали "Теорию вероятности" и "Мат. статистику". 1 человек изучал все три дисциплины и успешно их сдал. Сколько человек не сдали экзамена ни по одной из перечисленных дисциплин?
- # Из 5 девушек и 4 юношей нужно создать 2 команды по 2 пары. Каждая пара включает соответственно девушку и юношу. Сколькими способами это можно сделать?
- # Из 7 девушек и 5 юношей нужно создать 2 команды по 2 пары. Каждая пара включает соответственно девушку и юношу. Сколькими способами это можно сделать?
- # Из 7 девушек и 6 юношей нужно создать 2 команды по 3 пары. Каждая пара включает соответственно девушку и юношу. Сколькими способами это можно сделать?
- # На собрании должно выступить 5 человек: А, Б, В, Г и Д. Сколькими способами можно расположить их в списке ораторов при условии, что Б не должен выступать до того, как выступит А? [Большая Картинка]
- # На собрании должно выступить 6 человек: А, Б, В, Г, Д и Е. Сколькими способами можно расположить их в списке ораторов при условии, что Б не должен выступать до того, как выступит А?
- # На собрании должно выступить 7 человек: А, Б, В, Г, Д , Е и Ж. Сколькими способами можно расположить их в списке ораторов при условии, что Б не должен выступать до того, как выступит Д?
- # На собрании должно выступить 5 человек: А, Б, В, Г и Д. Сколькими способами можно расположить их в списке ораторов при условии, что оратор А должен выступить непосредственно перед оратором Б?
- # На собрании должно выступить 6 человек: А, Б, В, Г, Д и Е. Сколькими способами можно расположить их в списке ораторов при условии, что оратор А должен выступить непосредственно перед оратором Е?
- # На собрании должно выступить 7 человек: А, Б, В, Г, Д , Е и Ж. Сколькими способами можно расположить их в списке ораторов при условии, что оратор А должен выступить непосредственно перед оратором В? Б не должен выступать до того, как выступит Д?
- # Сколько можно сделать перестановок из 6 элементов, в которых данные 2 элемента "А" и "Б" не стоят рядом?
-
#
Сколько можно сделать перестановок из
![math]() элементов, в которых данные 2 элемента "А" и "Б" не стоят рядом?
элементов, в которых данные 2 элемента "А" и "Б" не стоят рядом?
- # На полке находятся 8 различных книг, из которых 3 в черных переплетах, а 5 в красных. Сколько существует перестановок этих книг, при которых книги в черных переплетах занимают первые три места?
- # На полке находятся 8 различных книг, из которых 3 в черных переплетах, а 5 в красных. Сколько положений, в которых все книги в черных переплетах стоят рядом?
-
#
На полке находятся
![math]() различных книг, из которых
различных книг, из которых ![math]() в черных переплетах, а
в черных переплетах, а ![math]() в красных. Сколько существует перестановок этих книг, при которых книги в черных переплетах занимают первые
в красных. Сколько существует перестановок этих книг, при которых книги в черных переплетах занимают первые ![math]() мест? Сколько положений, в которых все книги в черных переплетах стоят рядом?
мест? Сколько положений, в которых все книги в черных переплетах стоят рядом?
-
#
На полке находятся
![math]() различных книг, из которых
различных книг, из которых ![math]() в черных переплетах, а
в черных переплетах, а ![math]() в красных. Сколько положений, в которых все книги в черных переплетах стоят рядом?
в красных. Сколько положений, в которых все книги в черных переплетах стоят рядом?
- # Сколькими способами можно переставить буквы слова "перешеек" так , чтобы 4 буквы "е" не шли подряд?
- # Сколькими способами можно переставить буквы слова "огород" так , чтобы 3 буквы "о" не шли подряд?
- # Сколькими способами можно переставить буквы слова "барабан" так , чтобы 3 буквы "а" не шли подряд?
- # Сколькими способами можно переставить буквы слова "опоссум" так , чтобы буква "п" не шла непосредственно после буквы "о"?
- # Сколькими способами можно переставить буквы слова "бумага" так , чтобы буква "б" не шла непосредственно после буквы "у"?
- # Сколькими способами можно переставить буквы слова "колос" так , чтобы буква "с" не шла непосредственно после буквы "к"?
- # Сколькими способами можно переставить буквы слова "логарифм" так, чтобы ни одна буква не осталась на своем месте?
- # Сколькими способами можно переставить буквы слова "кино" так, чтобы ни одна буква не осталась на своем месте?
- # Сколькими способами можно переставить буквы слова "весна" так, чтобы ни одна буква не осталась на своем месте?
 ,
,  ,
,  - множество цифр (арабских).
- множество цифр (арабских).
 - множество чисел.
- множество чисел.
 и
и  .
Найти мощности этих множеств. Является ли множество
.
Найти мощности этих множеств. Является ли множество  подмножеством множества
подмножеством множества  ?
?
 и
и  . Равны ли они?
Записать элементы множества
. Равны ли они?
Записать элементы множества  , равного множествам
, равного множествам  и
и  .
Сколько вариантов записи множества
.
Сколько вариантов записи множества  .
Найти мощности этих множеств. Является ли множество
.
Найти мощности этих множеств. Является ли множество 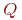 - множество двузначных чисел, являющихся степенями 2, которые нацело делятся на 5.
- множество двузначных чисел, являющихся степенями 2, которые нацело делятся на 5.
 и множества
и множества  ,
,  и
и  на рисунке. Записать элементы множеств
на рисунке. Записать элементы множеств  .
Представить эти множества графически.
.
Представить эти множества графически.
 и множества
и множества  . Составить булеан множества и определить его мощность.
. Составить булеан множества и определить его мощность.  . Составить булеан множества и определить его мощность.
. Составить булеан множества и определить его мощность.  . Составить булеан множества и определить его мощность.
. Составить булеан множества и определить его мощность.  . Найти множества:
. Найти множества:


 . Найти множества:
. Найти множества:

 . Найти множества:
. Найти множества:

 , а множество
, а множество  . Найти элементы множества
. Найти элементы множества  .
.  . Найти элементы множества
. Найти элементы множества  .
.  .
.  . Найти множество:
. Найти множество: 





 . Найти множество:
. Найти множество: 

 ?
?  ?
[Большая Картинка]
[Большая Картинка]
?
[Большая Картинка]
[Большая Картинка]
 ?
?  ?
?  )
) 
 . Найти прямое произведение
. Найти прямое произведение  .
.  . Найти прямое произведение
. Найти прямое произведение  .
.  и задано отношение
и задано отношение  . Записать отношение в явном виде.
. Записать отношение в явном виде.  и задано отношение
и задано отношение  . Записать отношение в явном виде .
. Записать отношение в явном виде .  и задано отношение
и задано отношение  . Выписать все элементы
. Выписать все элементы  и
и  .
.  и задано отношение
и задано отношение  . Выписать все элементы
. Выписать все элементы  и
и  и задано отношение
и задано отношение  . Найти тождественное и универсальное множества.
. Найти тождественное и универсальное множества.  . Найти тождественное и универсальное множества.
. Найти тождественное и универсальное множества.  . Найти тождественное и универсальное множества.
. Найти тождественное и универсальное множества.  и
и  . a) записать элементы множества
. a) записать элементы множества  . б). записать элементы отношения
. б). записать элементы отношения  ; в). найти область определения
; в). найти область определения  и область значений
и область значений  .
.  ; в). найти область определения
; в). найти область определения  ; в). найти область определения
; в). найти область определения  и область значений
и область значений  .
.  и задано отношение
и задано отношение  \rho = \left\{ {(-3, -3), (-3, -1), (-3, 1), (-3, 3),
(-1, -1), (-1, 1), (3, -3), (-1, -3), (1, -3), (1, -1)} \right\}. Каким способом представлено отношение на рисунке:
[Большая Картинка]
\rho = \left\{ {(-3, -3), (-3, -1), (-3, 1), (-3, 3),
(-1, -1), (-1, 1), (3, -3), (-1, -3), (1, -3), (1, -1)} \right\}. Каким способом представлено отношение на рисунке:
[Большая Картинка]

 . Каким способом представлено отношение на рисунке:
[Большая Картинка]
. Каким способом представлено отношение на рисунке:
[Большая Картинка]
 и задано отношение
и задано отношение  . Выписать все элементы
. Выписать все элементы  и задано отношение
и задано отношение  : a) записать отношение в явном виде; б)определить свойства отношения
: a) записать отношение в явном виде; б)определить свойства отношения  и задано отношение
и задано отношение  и задано отношение
и задано отношение  : a) записать отношение в явном виде; б)определить свойства отношения
: a) записать отношение в явном виде; б)определить свойства отношения  и задано отношение
и задано отношение  : a) записать отношение в явном виде; б) определить свойства отношения
: a) записать отношение в явном виде; б) определить свойства отношения  и задано отношение
и задано отношение  : a) записать отношение в явном виде; б) определить свойства отношения
: a) записать отношение в явном виде; б) определить свойства отношения  : a) записать отношение в явном виде; б) определить свойства отношения
: a) записать отношение в явном виде; б) определить свойства отношения  . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.  и задано отношение
и задано отношение  . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.  и задано отношение
и задано отношение  и задано отношение
и задано отношение  . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.  и задано отношение
и задано отношение  . Определить, какими свойствами обладает данное отношение.
. Определить, какими свойствами обладает данное отношение.  . Обладает ли данное отношение свойством эквивалентности?
. Обладает ли данное отношение свойством эквивалентности?  и задано отношение
и задано отношение  .Записать отношение в явном виде. Обладает ли данное отношение свойством эквивалентности?
.Записать отношение в явном виде. Обладает ли данное отношение свойством эквивалентности?  и задано отношение
и задано отношение  . Является ли оно функцией?
. Является ли оно функцией?  и задано отношение
и задано отношение  . Является ли оно функцией?
. Является ли оно функцией?  и задано отношение
и задано отношение  : a) является ли оно функцией? б) является ли оно отображением?
: a) является ли оно функцией? б) является ли оно отображением?  способами, т. е. всего вариантов . . . . .
способами, т. е. всего вариантов . . . . .  элементов, в которых данные 2 элемента "А" и "Б" не стоят рядом?
элементов, в которых данные 2 элемента "А" и "Б" не стоят рядом?  различных книг, из которых
различных книг, из которых  в черных переплетах, а
в черных переплетах, а